Abstract
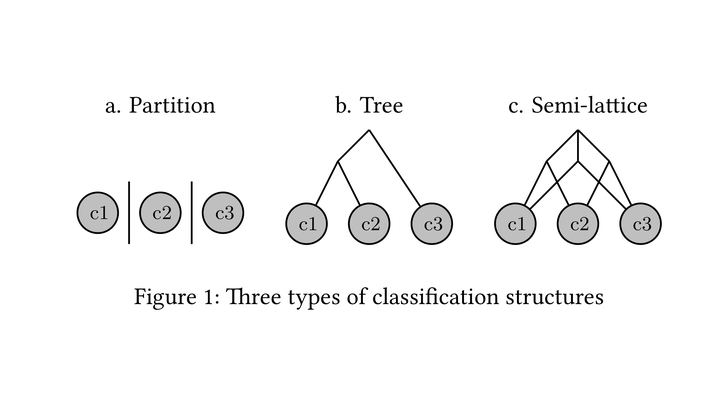
This paper discusses the nature of inflection classes (ICs) and provides a fully im- plemented methodology to conduct typological investigations into their structure. ICs (conjugations or declensions) are sets of lexemes which inflect similarly. They are often described as partitioning the set of lexemes, but similarities across classes lead some authors to favor hierarchical descriptions. While some formalisms allow for multiple inheritance, where one class takes after two or more others, it is usually taken as an exceptional situation. I submit that the structure of ICs is a typological property of inflectional systems. As a result, ICs are best modelled as semi-lattices, which by design capture non- canonical phenomena. I show how these monotonous multiple inheritance hierar- chies can be inferred automatically from raw paradigms using alternation patterns and formal concept analysis. Using quantitative measures of canonicity, I compare six inflectional systems and show that multiple inheritance is in fact pervasive across inflectional systems.